2-Variable K-Map
In any K-Map, each square represents a minterm. Adjacent squares always differ by just one literal (So that the unifying theorem may apply: X + X' = 1).
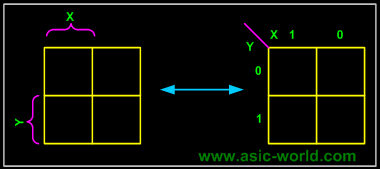
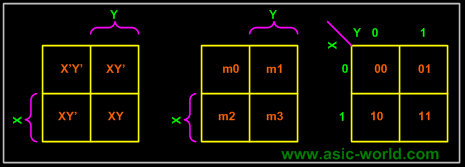
For the 2-variable case (e.g.: variables X, Y), the map can be drawn as below. Two variable map is the one which has got only two variables as input.

Equivalent labeling
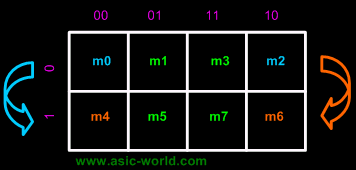
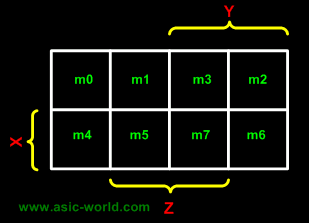
K-map needs not follow the ordering as shown in the figure above. What this means is that we can change the position of m0, m1, m2, m3 of the above figure as shown in the two figures below.
Position assignment is the same as the default k-maps positions. This is the one which we will be using throughout this tutorial.
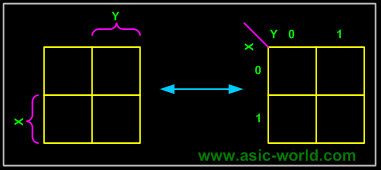
| This figure is with changed position of m0, m1, m2, m3. |
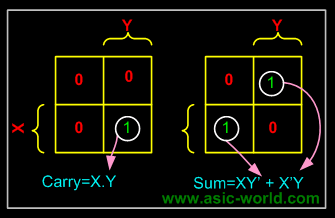
Example- Carry and Sum of a half adder
In this example we have the truth table as input, and we have two output functions. Generally we may have n output functions for m input variables. Since we have two output functions, we need to draw two k-maps (i.e. one for each function). Truth table of 1 bit adder is shown below. Draw the k-map for Carry and Sum as shown below.
.
| ||||||||||||||||||||
| Grouping/Circling K-map |
The power of K-maps is in minimizing the terms, K-maps can be minimized with the help of grouping the terms to form single terms. When forming groups of squares, observe/consider the following:
- Every square containing 1 must be considered at least once.
- A square containing 1 can be included in as many groups as desired.
- A group must be as large as possible.
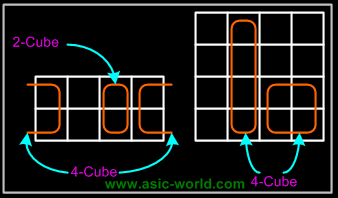
- If a square containing 1 cannot be placed in a group, then leave it out to include in final expression.
- The number of squares in a group must be equal to 2
- , i.e. 2,4,8,.
- The map is considered to be folded or spherical, therefore squares at the end of a row or column are treated as adjacent squares.
- The simplified logic expression obtained from a K-map is not always unique. Groupings can be made in different ways.
- Before drawing a K-map the logic expression must be in canonical form
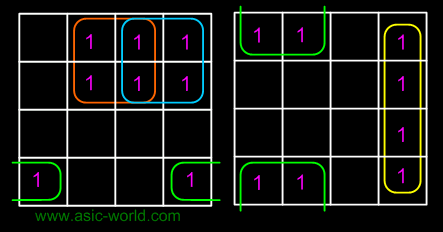
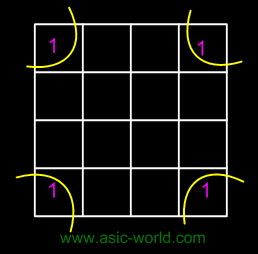
|
| In the next few pages we will see some examples on grouping. |
Example of invalid group
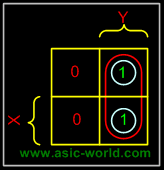
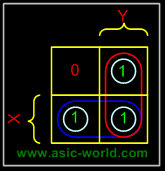
Example - X'Y+XY
In this example we have the equation as input, and we have one output function. Draw the k-map for function F with marking 1 for X'Y and XY position. Now combine two 1's as shown in figure to form the single term. As you can see X and X' get canceled and only Y remains.
F = Y
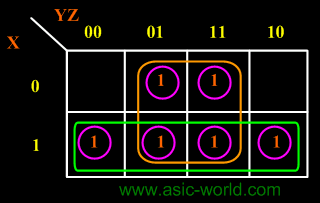
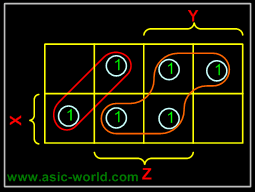
Example - X'Y+XY+XY'
In this example we have the equation as input, and we have one output function. Draw the k-map for function F with marking 1 for X'Y, XY and XY position. Now combine two 1's as shown in figure to form the two single terms.
F = X + Y
There are 8 minterms for 3 variables (X, Y, Z). Therefore, there are 8 cells in a 3-variable K-map. One important thing to note is that K-maps follow the gray code sequence, not the binary one.
Each cell in a 3-variable K-map has 3 adjacent neighbours. In general, each cell in an n-variable K-map has n adjacent neighbours.
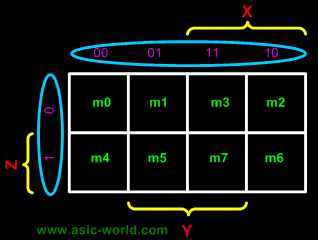
| There is wrap-around in the K-map | ||
| . |
| Â |
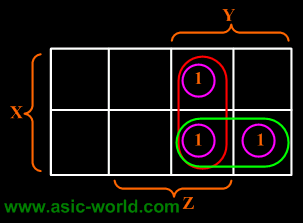
Example
| F = XYZ'+XYZ+X'YZ
|
| F = XY + YZ |
| Example |
| F(X,Y,Z) =
|
| F = X + Z |
Bạn Có Đam Mê Với Vi Mạch hay Nhúng - Bạn Muốn Trau Dồi Thêm Kĩ Năng
Mong Muốn Có Thêm Cơ Hội Trong Công Việc
Và Trở Thành Một Người Có Giá Trị Hơn
Mong Muốn Có Thêm Cơ Hội Trong Công Việc
Và Trở Thành Một Người Có Giá Trị Hơn