| | Adders are the basic building blocks of all arithmetic circuits; adders add two binary numbers and give out sum and carry as output. Basically we have two types of adders. |
 | Half Adder |
| | Adding two single-bit binary values X, Y produces a sum S bit and a carry out C-out bit. This operation is called half addition and the circuit to realize it is called a half adder. |
| | Truth Table |
| | | X | Y | SUM | CARRY | | 0 | 0 | 0 | 0 | | 0 | 1 | 1 | 0 | | 1 | 0 | 1 | 0 | | 1 | 1 | 0 | 1 | |
| | Symbol |
| | S (X,Y) = 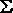 (1,2) (1,2) |
| | S = X'Y + XY' |
| | S = X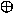 Y Y |
| | CARRY(X,Y) = 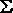 (3) (3) |
| | CARRY = XY |
| | Circuit |
| | 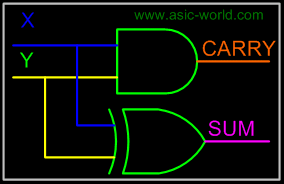 |
 | Full Adder |
| | Full adder takes a three-bits input. Adding two single-bit binary values X, Y with a carry input bit C-in produces a sum bit S and a carry out C-out bit. |
| | Truth Table |
| | | X | Y | Z | SUM | CARRY | | 0 | 0 | 0 | 0 | 0 | | 0 | 0 | 1 | 1 | 0 | | 0 | 1 | 0 | 1 | 0 | | 0 | 1 | 1 | 0 | 1 | | 1 | 0 | 0 | 1 | 0 | | 1 | 0 | 1 | 0 | 1 | | 1 | 1 | 0 | 0 | 1 | | 1 | 1 | 1 | 1 | 1 | |
| | SUM (X,Y,Z) = 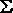 (1,2,4,7) (1,2,4,7) |
| | CARRY (X,Y,Z) = 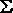 (3,5,6,7) (3,5,6,7) |
| | Kmap-SUM |
| | 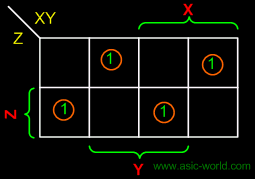 |
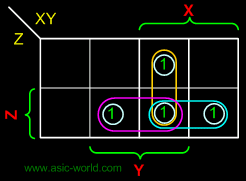
| | SUM = X'Y'Z + XY'Z' + X'YZ' |
| | SUM = X 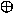 Y Y 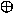 Z Z |
| | Kmap-CARRY |
| |  |
| | CARRY = XY + XZ + YZ |
 | Full Adder using AND-OR |
| | The below implementation shows implementing the full adder with AND-OR gates, instead of using XOR gates. The basis of the circuit below is from the above Kmap. |
| | Circuit-SUM |
| | 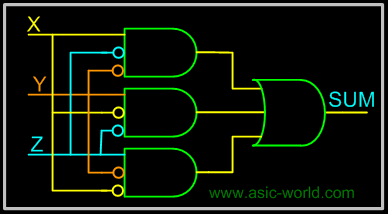 |
| | Circuit-CARRY |
| |  |
 | Full Adder using AND-OR |
| | Circuit-SUM |
| | 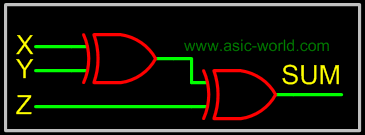 |
| | Circuit-CARRY |
| |  |