Decoders
A decoder is a multiple-input, multiple-output logic circuit that converts coded inputs into coded outputs, where the input and output codes are different; e.g. n-to-2n, BCD decoders
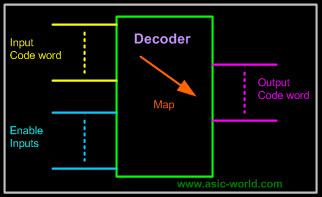
Enable inputs must be on for the decoder to function, otherwise its outputs assume a single "disabled" output code word.
Decoding is necessary in applications such as data multiplexing, 7 segment display and memory address decoding. Figure below shows the pseudo block of a decoder.
Basic Binary Decoder
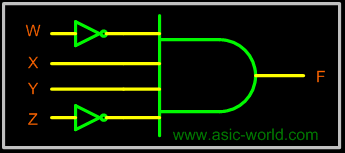
And AND gate can be used as the basic decoding element, because its output is HIGH only when all its inputs are HIGH. For example, if the input binary number is 0110, then, to make all the inputs to the AND gate HIGH, the two outer bits must be inverted using two inverters as shown in figure below.
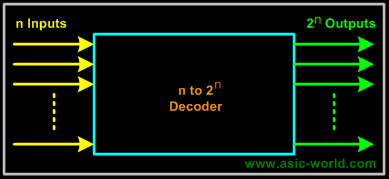
Binary n-to-2n Decoders
A binary decoder has n inputs and 2n outputs. Only one output is active at any one time, corresponding to the input value. Figure below shows a representation of Binary n-to-2n decoder
Example - 2-to-4 Binary Decoder
A 2 to 4 decoder consists of two inputs and four outputs, truth table and symbols of which is shown below.
Truth Table
| X | Y | F0 | F1 | F2 | F3 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
Symbol
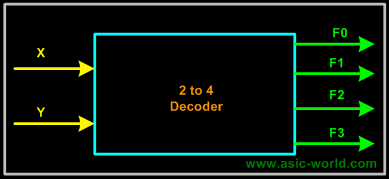
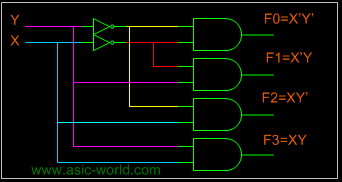
To minimize the above truth table we may use kmap, but doing that you will realize that it is a waste of time. One can directly write down the function for each of the outputs. Thus we can draw the circuit as shown in figure below.
Note: Each output is a 2-variable minterm (X'Y', X'Y, XY', XY)
Circuit
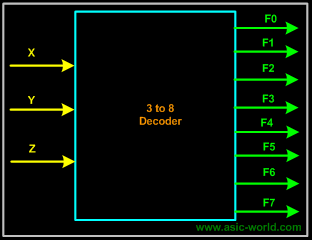
Example - 3-to-8 Binary Decoder
A 3 to 8 decoder consists of three inputs and eight outputs, truth table and symbols of which is shown below.
Truth Table
| X | Y | Z | F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Circuit
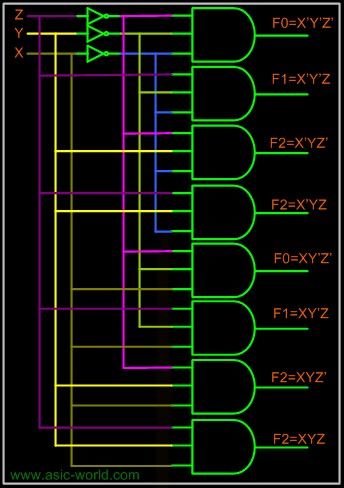
- Any n-variable logic function, in canonical sum-of-minterms form can be implemented using a single n-to-2n decoder to generate the minterms, and an OR gate to form the sum.
- The output lines of the decoder corresponding to the minterms of the function are used as inputs to the or gate.
- Any combinational circuit with n inputs and m outputs can be implemented with an n-to-2n decoder with m OR gates.
- Suitable when a circuit has many outputs, and each output function is expressed with few minterms.
Example - Full adder
Equation
| S(x, y, z) = | |||||
| C(x, y, z) = | |||||
| Truth Table | |||||
| X | Y | Z | C | S | Â |
| 0 | 0 | 0 | 0 | 0 | Â |
| 0 | 0 | 1 | 0 | 1 | Â |
| 0 | 1 | 0 | 0 | 1 | Â |
| 0 | 1 | 1 | 1 | 0 | Â |
| 1 | 0 | 0 | 0 | 1 | Â |
| 1 | 0 | 1 | 1 | 0 | Â |
| 1 | 1 | 0 | 1 | 0 | Â |
| 1 | 1 | 1 | 1 | 1 | Â |
From the truth table we know the values for which the sum (s) is active and also the carry (c) is active. Thus we have the equation as shown above and a circuit can be drawn as shown below from the equation derived.
Bạn Có Đam Mê Với Vi Mạch hay Nhúng - Bạn Muốn Trau Dồi Thêm Kĩ Năng
Mong Muốn Có Thêm Cơ Hội Trong Công Việc
Và Trở Thành Một Người Có Giá Trị Hơn
Mong Muốn Có Thêm Cơ Hội Trong Công Việc
Và Trở Thành Một Người Có Giá Trị Hơn
















